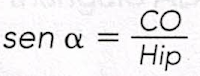El mundo geométrico: Teorema de Pitágoras

Recordemos que el teorema de Pitágoras surge de la relación entre los lados de un triángulo rectángulo. Para entender el procedimiento de este teorema es necesario recordar algunos conceptos importantes. Los lados se relacionan mediante el teorema de Pitágoras, el cual afirma que “la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa”. 

Del teorema anterior se desprenden los siguientes corolarios

1. En todo triangulo rectángulo la hipotenusa es igual a la raíz cuadrada de la suma de los cuadrados de los catetos. C² = a² + b²

 en donde: 

c: hipotenusa

a: cateto opuesto

b: cateto adyacente

Despejando la raíz cuadrada tenemos; 

2. En todo triángulo cada cateto es igual a la raíz cuadrada de la diferencia entre el cuadrado de la hipotenusa y el cuadrado del otro cateto. C² = a² + b²    

despejando el cateto opuesto. 

Despejando el cateto adyacente 

                      

Aplicando el teorema veremos los siguientes ejemplos:

1.- Determina el valor de la hipotenusa en el  siguiente triángulo rectángulo

2.- Encuentra la altura de un triángulo equilátero cuyos lados miden 10 m.

 En este caso se busca el cateto opuesto, se observa que en el segmento  BC se encuentra la línea recta que divide al triángulo (D), por lo que, para el cateto adyacente,  se toma el valor del segmento BD, el cual equivale a la mitad de lo que vale el segmento BC.

3.-  Determina el valor del cateto adyacente en el  siguiente triángulo rectángulo

  

Bibliografía 

Garrido Méndez Misael. (2015). Matemáticas II. Ciudad de México: SEP

El mundo geométrico: Razones trigonométricas

La trigonometría es la rama de las matemáticas que estudia las relaciones entre los lados y ángulos de cualquier triángulo. Desde hace más de 300 años los babilonios y los egipcios fueron los primeros en utilizar los ángulos y las razones trigonométricas para efectuar medidas en la agricultura, así como para la construcción de pirámides.

Etimológicamente la palabra trigonometría significa medida de los triángulos  con las raíces griegas (trígono) triángulo y metron (medida).  

(Garrido Méndez Misael. 2015), menciona que algunos puntos importantes para entender el comportamiento de las funciones trigonométricas son:

1. Un triángulo rectángulo tiene dos lados perpendiculares entre sí: a y b, que forman un ángulo recto (cuya medida es de 90°). Estos lados se denominan catetos del triángulo.
2. El tercer lado: c, opuesto al ángulo recto, se denomina hipotenusa del triángulo y su medida es mayor que la de los catetos. 
3. Los triángulos rectángulos tienen un ángulo interior de 90° y dos ángulos agudos complementarios (suman 90°). 
4. Para cualquiera de los ángulos agudos, un cateto es opuesto y el otro cateto es adyacente:
Para αA: el cateto a es opuesto y el cateto b es adyacente.  
Para αB: el cateto b es opuesto y el cateto a es adyacente.
5. Los lados se relacionan mediante el teorema de Pitágoras, que enuncia que “la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa”

 Los catetos se nombran según el ángulo agudo que se utilicen, recordemos que una razón trigonométrica esta en función del ángulo. 

Se denomina una razón trigonométrica cuando existe una relación entre los lados y ángulos de un triángulo rectángulo. Las razones trigonométricas más importantes son;   seno, coseno y tangente.

Las funciones naturales directas del ángulo son: 

Seno.- es la longitud de una semicuerda de una circunferencia de radio uno

Coseno.- complemento de una semicuerda en una circunferencia de radio igual a uno.

Tangente.- Recta que toca en un solo punto a una circunferencia de radio igual a uno.

Seno de un ángulo.-  es la razón entre el cateto opuesto y la hipotenusa

Coseno de un ángulo.- es la razón entre el cateto adyacente y la hipotenusa

Tangente de un ángulo.- es la razón entre el cateo opuesto y el cateto adyacente  

Las funciones naturales recíprocas del ángulo son: 

Cotangente de un ángulo.- es la razón entre el cateto adyacente y el cateto opuesto

Secante de un ángulo.- es la razón entre la hipotenusa y el cateto adyacente

Cosecante de un ángulo.- es la razón entre la hipotenusa y el cateto opuesto

De a cuerdo con (Aguilar Márquez Arturo, et al. 2009), sí un triángulo rectángulo se ubica en el plano cartesiano, de manera que uno de sus catetos coincida con el eje horizontal, las funciones trigonométricas tendrán un signo dependiendo del cuadrante sobre el cual se encuentre dicho triángulo, como se muestra a continuación: 

Signo de las funciones trigonométricas en un plano cartesiano. 

Fuente: Aguilar Márquez Arturo, et al.2009

Tabla de signos en una función trigonométrica de acuerdo a cada cuadrante en un plano cartesiano. 

Fuente: Aguilar Márquez Arturo, et al.2009.

Valor.-  dada una función trigonométrica de un ángulo agudo se 

pueden determinar las demás funciones a partir de la construcción de un triángulo rectángulo y el empleo del teorema de Pitágoras, ejemplo: 

1.- Si Ө es agudo y cosӨ =3/4  calcula los valores de las funciones trigonométricas para Ө

Solución: se construye un triángulo rectángulo, donde Ө es uno de los ángulos agudos, la hipotenusa es 4 y el cateto adyacente es 3. Se  aplica el teorema de Pitágoras para calcular el lado restante.

(4)² = (X)² + (3)³

16= X² +9

16-9 = X²

7 = X²

Por lo tanto las funciones trigonométricas para el ángulo Ө son:

2.- Sea el punto A (-3, 4) determina las funciones trigonométricas del ángulo α = < XOA.

Aplicando el teorema de Pitágoras

(OA)² = (-3)²  + (4)²

(OA)² = 9 +16       

Las funciones trigonométricas para el  α  son:

sen α = 4/5               cos α = -3/5       tan α = - 4/3 

        

cot α = -3/4              sec α = -5/3        csc α = 5/4

Ahora que has revisado la información resuelve los siguientes ejercicios

1.- Determina las funciones trigonométricas del ángulo que se muestra en la siguiente figura.

2.- Por el teorema de Pitágoras obtén la hipotenusa del siguiente triángulo rectángulo y determina las funciones trigonométricas 

3.- Determina las funciones trigonométricas del ángulo que se muestra en la siguiente figura.

Bibliografía

Aguilar Márquez Arturo, et al. (2009). Geometría y trigonometría. Naucalpan de Juárez, Estado de México: Prentice Hall.

Cordero Figueroa  Jenny, et al. (2019). Geometría y trigonometría. Naucalpan, edo. De México: esfinge.

Garza Olvera Benjamín. (2015). Geometría y trigonometría. México, DF.: PEARSON.

Garrido Méndez Misael. (2015). Matemáticas II. Ciudad de México: SEP

La química en nuestro entorno: mecanismos de transferencia de calor

                 Como hemos estudiado anteriormente, la energía está presente en un cuerpo y puede medirse mediante las escalas de temperatura Celsius, Kelvin y Fahrenheit, en esta ocasión,  trataremos acerca de los mecanismos de transferencia de calor, pero te has preguntado ¿Qué es el calor? o ¿Cómo se transmite el calor?

El calor  puede definirse como la presencia  de  energía en un cuerpo,  a medida que se incrementa dicha energía aumenta el calor, el método para medir la energía es a través de la temperatura utilizando un termómetro como herramienta de medición.

De acuerdo con (Smith-Van Ness. 1988), una de las observaciones más importantes sobre el calor es que siempre fluye de una temperatura superior a otra más baja, esto conduce al concepto de temperatura como fuerza impulsora para la transferencia de energía como calor.

La transferencia de calor puede darse de la siguiente manera:

Transferencia de calor por conducción.- este tipo de transferencia de calor  ocurre cuando  dos objetos están en contacto directo entre sí. Un ejemplo  de este tipo de transferencia de calor es cuando un metal está en  contacto directo con una fuente de calor. 

Transferencia de calor por convección.- Aquí la transferencia de calor ocurre cuando hay movimiento o circulación de energía entre los cuerpos en un sistema. Un ejemplo de este tipo de intercambio de energía lo podemos observar cuando abrimos un  horno caliente,  el calor que expulsa  hacia el exterior es la energía emitida por convección.

Transferencia de calor por radiación.- ocurre cuando hay contacto entre un objeto y las ondas electromagnéticas de un cuerpo. Un ejemplo de este tipo es el sol el cual sería el cuerpo  que emite radiación y un ser vivo como las plantas, los animales o seres humanos que están expuestos a la radiación solar.    

Calor específico 

El calor específico se define como la cantidad de calor requerida para elevar un grado Celsius la temperatura de una sustancia.
A continuación se muestra una tabla del calor especifico expresado en unidades de J/g°C   y   en cal/g °C en diferentes sustancias.

Fuente: (Navarro Herrera Dolores Adriana. 2019)

Para calcular el calor que necesita o produce un cuerpo se puede utilizar la siguiente formula:        Q = mC∆T

En donde:

Q: es  el calor absorbido  o liberado

m: es la masa de la sustancia

C: es el calor específico

∆T: indica la diferencia de temperatura (temperatura final, menos temperatura inicial)

Ahora veamos un ejemplo para calcular el calor  en una sustancia

1.- Obtén el calor absorbido por una muestra de 466g de agua que se calienta desde 8.5 °C hasta  74.6 ° C

Formula: Q = mC∆T

Datos

Q=?

m=466g

C = 1 cal/g °C

∆T = T_final – T_inicial  = (74.6 °C – 8.5 °C)

Se toma el valor del calor específico  para la sustancia en este caso el agua (1 cal/g °C).

Sustituyendo datos:

Q = (466g) (1 cal/g °C) (74.6 °C – 8.5 °C)      

Al realizar las operaciones se eliminan las unidades de masa (g) y las  unidades de temperatura °C quedando únicamente calorías

Q =30 802.6 calorias

Revisa el siguiente vídeo donde se explica paso a paso el problema planteado. 

Las reacciones pueden absorber o liberar calor clasificándose en:

Reacción endotérmica.- es aquella reacción que absorbe calor del exterior, los reactivos tienen menor energía que los productos,  por ejemplo,   en la fotosíntesis  que realizan  las plantas se necesita la energía solar para que se pueda  llevar a cabo el proceso.

Reacción exotérmica.- es aquella reacción que libera calor al exterior, aquí los reactivos tienen mayor energía que los productos por lo que desprenden calor  un  ejemplo de este tipo de reacciones es  la combustión. 

Revisa el siguiente video cuestionario Mecanismos de transferencia de calor

 Ahora que has revisado la información resuelve los siguientes ejercicios (consulten la tabla de calores específicos descrita anteriormente para obtener el valor del calor especifico de acuerdo a la sustancia en cada problema, utilicen el valor con la unidad  cal/g °C )

1.- Calcula la cantidad de calor liberado por 30g de aluminio cuando se enfría desde              77 °C hasta 12 °C

2.- Calcula el calor que libera 4 g de hierro sí se enfría desde 50 °C hasta 15 ° C

3.- Calcula el calor absorbido por una muestra de 30g de etanol si se calienta desde                9° C hasta 36 °C

4.- Calcula el calor especifico del estaño si una muestra de 20g se calienta desde                     10 °C hasta 55 °C  absorbe 204. 3 calorías    

Bibliografía

Navarro Herrera Dolores Adriana. (2019). Química II. Naucalpan, Edo. De México: Esfinge

Smith-Van Ness. (1988). Introducción a la termodinámica en ingeniería química. México, D.F: Mc Graw Hill.    

El mundo geométrico: Teorema de Tales

Tales de Mileto (623-540 a.c) fue un astrónomo, geómetra, filósofo y estadista griego introdujo el estudio de la geometría deductiva, este método consiste en encadenar conocimientos que se suponen verdaderos de tal manera que se obtienen nuevos conocimientos, es decir, obtener nuevas proposiciones como consecuencia lógica de otras anteriores. Hizo aportaciones importantes al pensamiento científico y racional, a la física, teología y principalmente a la geometría, una de estas aportaciones lleva su nombre. (Cordero Figueroa  Jenny, et al. 2019). 

El teorema de Tales establece lo siguiente: “Si tres o más paralelas cortan a dos transversales o secantes, determinan en ellas segmentos correspondientes proporcionales”. 

Teorema de Tales  aplicado en el triángulo

Si se traza una paralela a un lado de un triángulo, que corte a los otros dos lados, entonces estos quedan divididos en segmentos proporcionales.  

Reciproco del Teorema de Tales

Sí al trazar una recta que corta dos lados del triángulo rectángulo se forman segmentos proporcionales, entonces la recta es paralela al tercer lado.

 

Entonces las rectas DE y AB son paralelas

Ejemplo: sí las rectas DE Y AB son paralelas y si la razón de los segmentos CE  y CB es 3/4  ¿ Cuál es la razón de los segmentos CD y DA? ¿Cuanto mide CD?
La respuesta a la primera pregunta se justifica por el teorema de Tales  y su resultado es 3/4 . 

Para determinar la medida del segmento CD, el planteamiento de la siguiente proporción se resuelve de la siguiente manera: 

Bibliografía 

Cordero Figueroa  Jenny, et al. (2019). Geometría y trigonometría. Naucalpan, edo. De México: esfinge.

Garrido Méndez Misael. (2015). Matemáticas II. Ciudad de México: SEP.